Iz opisa Transformation Pipeline postupka se vidi da koordinate po?etnog modela bivaju transformisane vi?e puta dok se ne formira kona?na slika. Ovo zna?i da je za rad sa 3D objektima potrebno obezbediti (implementirati) transformacije objekata kao ?to su: translacija, rotacija, skaliranje i projekcija.
Iako se za specijalne probleme i zadatke koordinate mogu transformisati jednostavnim izra?unavanjima, linearna algebra nam daje znanje koje nam omogu?ava da za op?ti slu?aj sve ove transformacije izvedemo koriste?i matrice.
Da bi se koristile matrice tranformacija potrebno je da koordinate budu u obliku homogenih koordinata [(x, y, z, w)], a matrice transformacije se defini?u kao matrice dimenzija 4x4.
Ovde se, kao ?to je na po?etku re?eno, pretpostavlja odre?eno predznanje iz linearne algebre tako da se ne?e iznositi teorija koja defini?e homogene koordinate, potrebu za njihovom uvo?enjem i kreiranjem matrica transformacija.
S druge strane ?e biti obja?njeno kako ove matrice koristiti u prakti?nom radu.
Ako se pretpostavi da je zadatak translirati objekat za vektor (Tx, Ty, Tz) matrica translacije je u tom slu?aju:
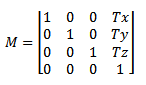
Mno?enjem matrice i vektora koji predstavlja koordinatu (x, y, z, w) dobija se nova, translirana, koordinata.
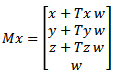
Sli?no, ako je potrebno rotirati objekat ili celu scenu koristi?e se matrica rotacije, za potrebe zumiranja ?e se koristiti matrica skaliranja, a za projekciju na 2D ravan odgovaraju?a matrica projekcije.
Da bi se moglo iskoristiti predstavljanje transformacija preko matrica potrebno je da programer kreira sve potrebne matrice, da obezbedi implementaciju mno?enje matrica kao i sve ostale operacije sa matricama koje ?e mu biti potrebne s obzirom da WebGL nema ugra?enu ovu funkcionanost. Ovo bi zna?ilo da programer ima zadatak da napi?e vrlo op?tu biblioteku za rad sa matricama. S obzirom da u kompjuterskoj grafici (jo? uvek) znatno uti?e brzina izvr?avanja operacija mo?e se jo? zaklju?iti da bi bilo potrebno i da ova biblioteka bude prili?no kvalitetno i optimizovano implementirana.
Zbog svega ovoga se naj?e??e koriste gotove biblioteke za rad sa matricama, koje postoje na tr?i?tu i koje nam obezbe?uju sve potrebne funkcionalnosti, pogotovo u procesu u?enja i kod jednostavnijih zadataka
U ovom radu ?e se koristiti popularna biblioteka gl-matrix.
Ova biblioteka je ?iroko rasprostanjena, dobrih performansi i dovoljno testirana, a i mnogi referentni resursi (web sajtovi i knjige) koji se koriste za u?enje WebGL-a koriste upravo ovu biblioteku tako da izbor ove biblioteke u potpunosti odgovara ciljevima ovog rada.
U prethodnom primeru se iscrtavao kvadrat.

Ovde ?emo taj kvadrat translirati za 0.2 ta?aka po x osi.

Prvo je potrebno preuzeti i referncirati biblioteku.
<script type="text/javascript" src="../libs/gm/gl-matrix-min.js"></script>
Odgovaraju?a matrica translacije se kreira funkcijom translate biblioteke glMatrix.
Prethodno se matrica kreira funkcijom create koja je pri tom postavlja na identi?nu matricu dimenzije 4.
var mvMatrix;
function initMatrices()
{
mvMatrix = mat4.create();
mat4.translate(mvMatrix, mvMatrix, [0.2, 0, 0]);
}
Matrica u primeru je nazvana mvMatrix ?to je ?irko prihva?ena konvenciija za ozna?avanje matrice koja predstavlja proizvod translacije, rotacije i skaliranja.
mv je skra?enica od Model-View ?to ukazuje na to da ?е se u njoj nalaziti proizvod prva tri koraka iz Transformation pipeline-a.
Vertex shader se menja tako da se ovaj put gl_Position ra?una kao proizvod matrice transformacije, koja u ovom slu?aju sadr?i samo translaciju,
i vektora koji sadr?i podtake o vertex-u. Na ovaj na?in ?e svaki vertex biti transliran, a samim tim i cela figura.
<script id="shader-vertex" type="x-shader/x-vertex">
attribute vec3 vpos;
uniform mat4 mvMatrix;
void main() {
gl_Position = mvMatrix * vec4(vpos, 1);
}
</script>
Re?eno je da se za prenos vrednosti u shader koriste atributi (vpos).
Pored atributa postoje i uniform promenljive.
Ove promenljive povezuju shader, WebGL i aplikaciju i predstavljaju promenljive za ?uvanje vrednosti koji se ne menjaju sve dok se izvr?ava jedno iscrtavanje.
Zato se za prosle?ivanje matrice transformacije shader-u koristi uniform promenjiva (vpos dobija vrednosti iz niza, a matrica je ista za sve vertex-e).
Nakon linkovanja shader programa u aplikaciji, sli?no kao za atribut vpos, potrebno je preuzeti referencu na deo memorije gde se nalazi uniform promenljiva u koju treba upisati vrednost matrice.
function drawScene() {
var positionLocation = gl.getAttribLocation(shaderProgram, "vpos");
gl.enableVertexAttribArray(positionLocation);
gl.vertexAttribPointer(positionLocation, 3, gl.FLOAT, false, 0, 0);
var sh_mvMatrixUniform = gl.getUniformLocation(shaderProgram, "mvMatrix");
gl.uniformMatrix4fv(sh_mvMatrixUniform, false, mvMatrix);
gl.drawArrays(gl.TRIANGLE_FAN, 0, 4);
}
Ovim jednostavnim uklju?ivanjem matrice transformacije u izra?unavanje dobija se translirani kvadrat.
Mogu?e je da je do sada po?etnicima delovalo da je za kreiranje ovako jednostavnih rezultata potrebno dosta truda.
Me?utim, do sada formirani programski okvir za aplikaciju se mo?e skoro neizmenjen koristiti, a jednostavnim promenama transformacija i temena se mogu dobiti razli?iti rezultati. ?ak i rad sa 3D figurama (u narednom poglavlju) ne?e uvesti zna?ajnije promene u konceptu i kodu aplikacije. Tako da se u ovom momentu ve? polako mo?e naslutiti koje su prednosti kori??enja shader-based jezika i koliko je takav koncept mo?an.
* Ukoliko budete prou?avali primere na internetu koji koriste biblioteku glMatrix obratite pa?nju na to koju verziju biblioteke koristi autor. Od aprila 2013 je dostupna verzija 2.0 koja nije kompatibilna sa prethodnim verzijama.
* U GLSL mo?ete korisiti operator * za mno?enje matrica, u JavaScript-u ne mo?ete.
* U vezi sa prethodnim: Kad se radi u WebGL, u shaderima, prilikom mno?enja matrica se koriste nizovi u kojima su matrice predstavljene tako ?to se kolone nalaze jedna za drugom. Vodite o ovome ra?una ukoliko koristite biblioteku za rad sa matricama koja vra?a matricu kao niz gde su vrednosti date red-po-red. U tom slu?aju ?et morati da izvr?ite prethodno transponovanje matrice.
* Jo? jedno upozorenje za copy-paste. WebGL je izveden iz Open ES 2.0. OpenGL ES 2.0, kao i OpenGL 3.2+ nemaju standardne funkcije sa matricama u svom API-ju za razliku od prethodnih verzija OpneGL-a ?to mo?e da dovede do zabune ukoliko se koriste ranije napisane funkcije.